2 minute read

> Go to Data Science Contents

Linear classification

Point들이 어떤 class에 속해있는지 구하기

Classification Tasks

  • Regression tasks: predicting real-valued quantity $y \in \mathbb{R}$
    • R안에 있는 real value 구하기
  • Classification tasks: predicting discrete-valued quantity y
    • 이산적인 value 구하기
  • Binary classification: $y \in {-1, +1}$
  • Multiclass classification: $y \in {1, 2, …, k}$

Features를 잘 만드는 것이 중요하다!

  • 구분을 지을 수 있는 유의미한 데이터: features

Example: Breast Cancer Classification

유방 종양 양성 악성 진단 모델

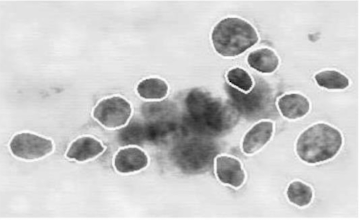
각각의 cell은 area, perimeter, concavity, texture로 Feature를 추출할 수 있으며, 각각의 feature들을 Mean/std/max로 만들 수 있다.
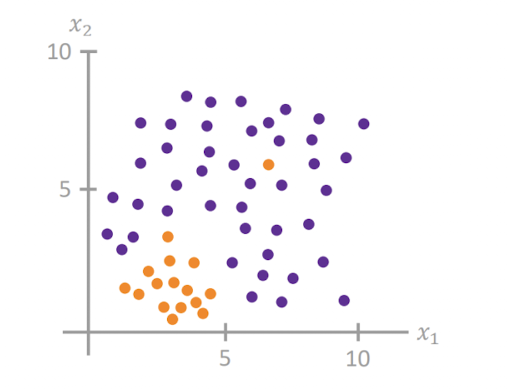
2개의 features: mean area vs mean concave point

뭔가 Linear하게 나눌 수 있을 것 같음. 그러나 우리의 최종 목표는 classification하는 것.
Linear classification $\equiv$ “drawing line separating classes”
즉 클래스를 나누는 선을 그리는 것.


sign함수를 사용하여 한쪽 방향에 있으면 양수, 아니면 음수가 되도록 만든다.

그럼 Loss는 어떻게 구할까? square loss?

0/1 Loss

sign함수가 같은 label이라면 0, 아니라면 1(Loss값을 부여함)을 준다.

\begin{align} \ell_{0/1}(h_\theta (x), y) = \begin{cases} 0, \text{if sign} (h_\theta (x)) = y& \newline 1, \text{otherwise}& &\newline \end{cases} \nonumber \end{align}

그러나 0/1 loss는 optimize하기 힘들다 (NP-Hard)

Logistic Regression

$Sigmoid Function$ 사용!
클수록 1에 가깝고, 작을수록 0에 가까움

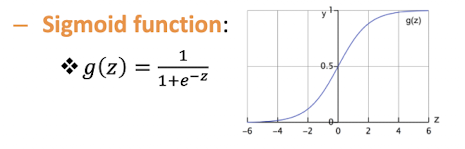
아까의 Hypothesis Function을 Sigmoid function에 태우자!

  • $h_\theta (x) = g(\theta^T x) = \frac{1}{1+e^{-\theta^T x}}$

  • Logistic Loss (cost function)
    간단하게 y가 1일때 0에 가까우면 cost가 높고, 반대의 경우도 같은 형태로 계산된다.
    한줄로 표현하면 다음과 같이 표현할 수 있다. $Cost(h_\theta(x), y) = -y\log (h_\theta(x)) - (1-y)\log(1-h_\theta(x))$

Evaluation of Classification

Confusion matrix: 예측값이 실제값 대비 얼마나 잘 맞는지 행렬로 표현

  True라 예측 False라 예측
True True Positive False negative
False False Positive True negative
  • 정확도 (accuracy): 전체 데이터 개수 대비 정답을 맞춘 데이터 개수
    $Accuracy = \frac{TP+TN}{TP+TN+FP+FN}$
  • 정밀도 (precision): 모델이 1이라고 예측했을 때 얼마나 잘 맞을지
    $Precision(PPV) = \frac{TP}{TP+FP}$

  • 민감도 (Recall, sensitivity): 실제 1인 값을 모델이 얼마나 잘 1이라고 예측했는지
    $Recall(TPR) = \frac{TP}{TP+FN}$

  • F1 Score: 정밀도와 민감도의 조화 평균 값 $F_1 = 2 \times \frac{precision \times recall}{precision + recall}$

Threadhold

Sigmoid함수에 hypothesis를 넣으면, 0~1값이 나온다. 여기서 0과 1을 구분짓는 기준을 뭐로 둬야하나? => Threadhold값!
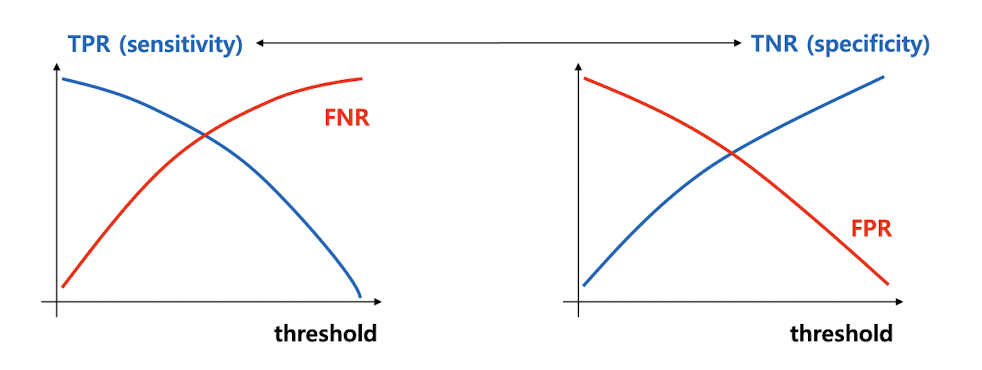
Threadhold값이 높을수록? 높은 값만 신뢰하겠다. (0.99값 이상만 믿겠다)

ROC Curve

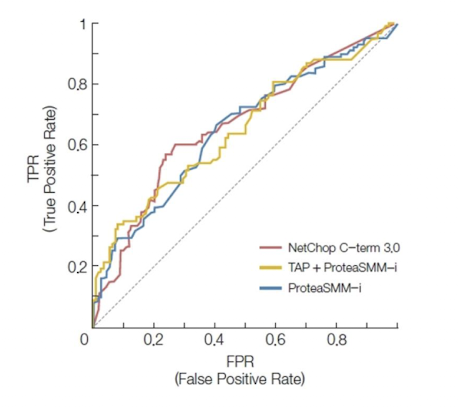
ROC(Receiver Operating Characteristics) Curve: TPR과 FPR을 각 축으로 그래프로 나타내는 커브
하나의 ROC Curve: 하나의 모델의 Thread curve를 바꿔가면서 결과를 나열한 것
밑이 넓을 수록 좋은 모델!

AUC

AUC(Area Under the Curve): ROC curve 하단의 넓이

Decision tress

Decision trees: “Understandable” ML algorithm
(해석 가능한 머신러닝 알고리즘)
if ~ else 와 같은 방식으로 절차적인 결정을 트리 구조로 해나감

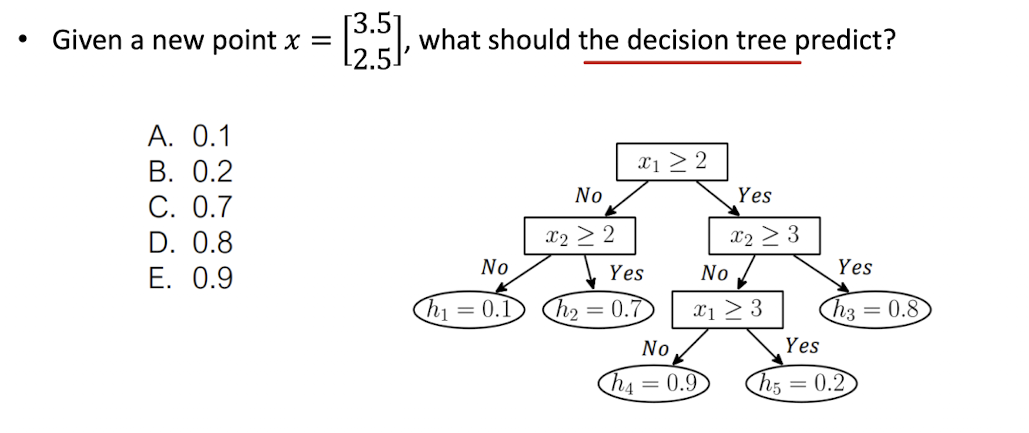
Rule에 의해서 리프노드까지 뻗어나간다.

Training (classification) decision trees

  1. What is the hypothesis function $h_\theta(x)$?
    • 트리 구조로 되어있다.
  2. What is the loss function $\ell(h_\theta(x), y)$?
    MLE! Loss function은 출력 값의 negative log probability이다.
    $\ell(h_\theta(x), y) = -\log p(y|h_\theta(x)) = -y\log h_\theta(x) - (1-y)\log(1-h_\theta(x))$
  3. How to we minimize the loss function?
    $\underset{\theta}{\text{minimize}} \frac{1}{m}\sum_{i=1}^{m}\ell(h_\theta (x^{(i)}), y^{(i)})$
    discrete tree structue는 미분이 불가능 하다! 각각의 노드에 각각 decision tree를 최적화 한다.

Optimizing a Single Leaf

그러면 Leaf node를 만드는 선을 어떻게 그려야 하나?
Entropy (불순도, 불확실성, 정보량) = $-\sum_i p_i \log p_i$

Gini impurity (지니 불순도): 엔트로피 대체
$G = 1-\sum_{i=1}^{n} p_i^2$

Boosting

Ensemble model을 많이 사용함!

You May Also Enjoy